There might be some simple explanation but i cannot figure it out.
You can’t just add the balances and expect it to amount to the same as the spend. Consider this: you spend 0, 0, 0, 50. Your balances are 50, 50, 50, 0. Adding up the balances you get 150. What does this mean? Absolutely nothing.
Maybe 1, 1, 1 -> 49, 48, 47 is a better example though. But same thing.
I wanted to keep it simple and avoid a factorial sum. My example also shows that the remainder sum goes up even when nothing is spent.
“I am your father’s brother’s nephew’s cousin’s former roommate”
“What’s that make us?”
The balance has no reason to add up to 50. So there is no extra anything. If you kept spending 1 each row, and then summed the balance at the end, it would be massively higher than the 50 you started with.
Yeah you’re right
deleted by creator
This calculation is a bit wrong.
Lets say for example you keep spending 5 after your first payment, then your totals at the bottom would be wrong and would look like this.
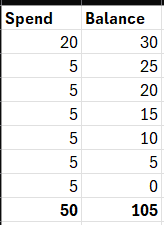
The correct way to do this is to accumulate the expenditure as your balance goes down, so that total for both spend and balance equals 50.

I hope this makes sense.
Summing a balance column is never correct. Take any example that doesn’t end in a zero balance and it’s easy to see that the balance column’s sum is meaningless:

The sum of spend will always be $50.
The sum of balance doesn’t mean anything and reflects the number of transactions rather than their size.
Do the same thing again spending $1 at a time and you’ll see.
OMG I do math all the time and the way the question was phrased I fell for it. (Summing balance)
I’m going to feel dumb for the rest of the day.
Data scientist here! What you have discovered is what’s known in data analytics as a semi-additive measure. Instead of summing the balance column, you would count it, and get a measure that showed how many transactions took place, but not a balance. Of course, there’s no reason to simply count the one column, a row count would suffice and return the same.
add a “spend 0 / balance 50” column
There’s no reason to expect that the sum of the balances remaining would be equal to the initial amount. If you spend in 1$ increments, the balances would be 49, 48, 47,… which sum to much larger than 50. If you spend 49$ followed by 1$, right away, the balances sum to 1$, which is much less than 50. This particular example has been “cooked” to give a value of 51. You can cook up another example to give whatever value you want.
Adding up the balance column doesn’t make sense to do in the first place.
Watch this and it should clear things up.
Am I missing something here? The numbers are different between the columns. The “extra 1” comes from the 30.
Put the 50 where the word balance is, and go diagonal. 50-20=30, 30-15=15, 15-9=6, 6-6=0
Remember in school when they made a big deal about the order of operations? This is why. It’s not clear as to why, as you’re not seeing the entire picture though, just some numbers.
This has nothing to do with order of operations.









